Self-Organizing Maps

Abstract

Le Self-Organizing Maps sono una tipologia di reti neurali allenate utilizzando apprendimento non supervisionato per produrre una rappresentazione (di solito una mappa bidimensionale) dello spazio dei dati in input.

Ciò rende le SOM un valido strumento per l’analisi esplorativa dei dati: in particolare sono molto utili per visualizzare i dati, analizzarne la tendenza di clustering e studiare le relazioni esistenti tra le variabili del dataset.

Idea e concetti principali

In questo articolo verranno illustrate le Self-Organizing Maps, uno strumento di apprendimento automatico non supervisionato per l’analisi dei dati, con l’obiettivo di rappresentare la distribuzione dei dati in input usando un insieme finito di modelli (anche chiamati prototipi o codebooks) organizzati spazialmente su una mappa di solito bidimensionale.

Si tratta di uno strumento utile per i data scientist durante la fase di exploratory data analysis (EDA), in particolare per le fasi di identificazione degli outliers (osservazioni anomale), di visualizzazione dei dati e di comprensione delle relazioni esistenti tra le variabili del dataset. Inoltre, risulta anche efficace per farsi un’idea della tendenza di clustering dei dati: la mappa si può utilizzare sia come strumento per determinare il numero di cluster presente nei dati, sia per valutare la bontà dei raggruppamenti ottenuti da un algoritmo di clustering.

La mappa prodotta in output da questo strumento può, infatti, essere visualizzata in diverse modalità:

• Colorando i codebook secondo il valore di una variabile del dataset: questa visualizzazione è molto utile per comprendere la distribuzione di probabilità della variabile e, inoltre, analizzando le mappe colorate con diverse variabili, è possibile avere un’intuizione riguardo le interdipendenze tra variabili;
• Colorando la mappa secondo la distanza euclidea tra codebook adiacenti: questa visualizzazione prende il nome di U-matrix (unified distance matrix) ed è molto utile per comprendere la tendenza di clustering dei dati. Colori scuri, infatti, rappresentano codebook molto vicini nello spazio dei dati in input e colori più chiari indicano nodi separati da più spazio: gruppi di codebook di colore scuro possono essere considerati cluster, mentre le aree più chiare sono i confini tra cluster.

Per questo motivo, le Self-Organizing Maps risultano uno strumento molto versatile, che permette un’esplorazione semplice ed intuitiva dei dati in analisi. Questa grande versatilità permette di utilizzarle in diversi domini: infatti si trovano esempi di applicazioni in diversi ambiti, tra cui quello finanziario, marketing, assicurativo.

L’output delle SOM ricorda quello che si ottiene con la classica Vector Quantization (VQ), una tecnica ampiamente utilizzata in ambito di digital signal processing. Con la VQ, lo spazio vettoriale costituito dai vettori dei dati in input (cioè le features che descrivono i dati), è partizionato in un numero finito di regioni contigue: ogni regione è rappresentata in maniera ottimale da un unico vettore che funge da modello, chiamato codebook. Per ottenere un partizionamento ottimale, i codebook sono costruiti in maniera tale per cui la distanza media (secondo una metrica di interesse) di un dato in input dal codebook che lo rappresenta, chiamato codebook vincitore, è minimizzata.

A differenza della Vector Quantization, però, nell’algoritmo SOM i codebook sono associati automaticamente coi nodi di una griglia regolare ordinata (di solito bidimensionale). I prototipi risultano quindi ordinati spazialmente sulla mappa, in modo che prototipi con caratteristiche simili (secondo le features che descrivono i dati) siano associati a nodi adiacenti nella griglia.

Questa organizzazione globale costituisce una sorta di diagramma di similarità dei codebooks e permette di ottenere un’idea delle relazioni topografiche esistenti nei dati. Le Self-Organizing Maps possono essere infatti considerate una tecnica di riduzione della dimensionalità che mantiene la topologia dello spazio vettoriale originale dei dati (per topologia si intendono le proprietà geometriche che si conservano sotto deformazioni continue).

Durante l’allenamento, le SOM formano una griglia elastica che si adatta alla forma della nuvola dei dati nello spazio vettoriale originale. Le osservazioni vicine nello spazio vettoriale originale sono mappate con codebooks vicini nella mappa, come si può vedere nella seguente immagine:

L’algoritmo è una rete neurale artificiale: i nodi della mappa sono infatti i neuroni del livello finale della rete neurale della SOM. In particolare queste reti neurali vengono allenate tramite competitive learning: per ogni vettore di input, i neuroni competono tra loro per identificare quello più simile a quel particolare vettore di input. Una volta identificato il neurone (o nodo) vincente, i prototipi della mappa vengono modificati per assomigliare al vettore di input. In particolare, le modifiche interesseranno il prototipo vincente ed i nodi ad esso adiacenti nella mappa (l’impatto della modifica dipende infatti da una funzione kernel centrata sul nodo vincente): in questo modo i nodi della mappa si specializzano per replicare le caratteristiche dei dati originali. Le mappe vengono definite self-organizing per questo motivo: l’intero allenamento avviene in maniera non supervisionata.

L'algoritmo

L’algoritmo di training delle SOM, presentato di seguito, è euristico, iterativo e batch-type. La formulazione originaria dell’algoritmo è stata provata solo a livello teorico in alcuni spazi a bassa dimensionalità.

L’algoritmo prevede i seguenti passaggi:

Inizializzazione dei codebook, due metodologie:

• vengono assegnati valori di vettori di input presi casualmente da set di training;
• viene assegnata una sequenza di valori presi dall’iperpiano attraversato dalle prime due componenti principali (PCA): migliore strategia in quanto questi valori sono già una buona approssimazione dei pesi della SOM e si velocizza la fase di training;

dato un vettore di input x(t) dal set di training, trova il codebook m_i(t) più vicino a x(t):

• compute c = argmini(∥ x(t)-m_i(t) ∥)
• c è l’indice del coodbook vincente (chiamato anche Best Match Unit - BMU)

Il codebook vincente e i codebook vicini vengono modificati in una direzione tale che i modelli modificati si abbineranno meglio con l'input x(t):

• m_i(t+1) = m_i(t) + α(t) h_ci(t) [x(t) - m_i(t)]
• h_ci(t) è la neighborhood function che definisce l’impatto delle trasformazioni sui codebook vicini: tanto più un codebook è vicino al BMU tanto più elevato sarà l’impatto della trasformazione;
• h_ci(t) decresce con t;
• α(t) coefficiente di adattamento che decresce con t;

Ripetere gli step 2-3 per ogni vettore di input;

Fine prima epoca

Per ogni epoca si ripetono questi passaggi, l’inizializzazione non è più random ma i pesi dei codebook sono determinati dai risultati dell’epoca precedente.

SOM per segmentazione della clientela

La segmentazione della clientela è uno dei campi di applicazione delle SOM nel settore CRM. L’elemento chiave nel CRM e nella segmentazione dei clienti è l’informazione generale sui clienti. Oggi i dati sui clienti sono prontamente disponibili tramite ERP, data warehouse aziendali e internet. Il problema è che la quantità di informazioni disponibili per la segmentazione è enorme e può essere molto impegnativa da gestire. Perciò, l’estrazione delle informazioni provenienti da grandi database è spesso eseguita utilizzando metodi di data mining.

In questo contesto, le SOM costituiscono uno strumento molto utile sia nella fase di exploratory data analysis (EDA) sia nella vera e propria fase di segmentazione, il clustering. In EDA, le SOM consentono di visualizzare sulla mappa le caratteristiche dei consumatori prima di effettuare il clustering: è possibile valutare già in fase esplorativa quali consumatori sono simili e quali caratteristiche li rendono simili. Il clustering viene effettuato sui codebook stimati dalle SOM ed identifica dei gruppi le cui caratteristiche possono essere facilmente estratte dall’osservazione della mappa. Questo approccio, calcolo delle SOM e clustering dei codebook delle SOM, viene chiamato “a due livelli”.

Quindi, utilizzare le SOM per la profilazione e la segmentazione della clientela fornisce due principali vantaggi:

• Osservando la mappa si possono facilmente visualizzare e comprendere le caratteristiche dei clienti analizzando le caratteristiche dei codebook che formano la mappa.
• Organizzando i clienti in una SOM vengono clusterizzati i codebook e non i dati di input. I dati di input vengono, quindi, associati al cluster assegnato al proprio BMU. In questo modo è possibile esplorare le relazioni tra i raggruppamenti generati dall’algoritmo di clustering.

Vediamo di seguito le analisi e i risultati dell’algoritmo SOM applicati a dei dati di vendita di un supermarket (vedi dataset Kaggle).

Il dataset originale è stato ristrutturato in modo tale da avere per ciascun cliente:

• Spesa media per transazione
• Quantità media di prodotti acquistati per transazione
• Range di età

L’algoritmo SOM supporta solo valori numerici, perciò è necessario codificare le variabili categoriali. In questo esempio, per ciascun range di età è stata creata una variabile dummy (1 = cliente appartiene a quel range di età, 0 = altrimenti).

Inoltre, l’algoritmo è molto sensibile alla presenza di outliers: è importante verificarne la presenza e ridurne l’impatto. In questo esempio, le distribuzioni delle variabili spesa media e quantità media di prodotti acquistati sono molto distorte a causa della presenza di outliers, perciò sono state trasformate con una funzione logaritmica.

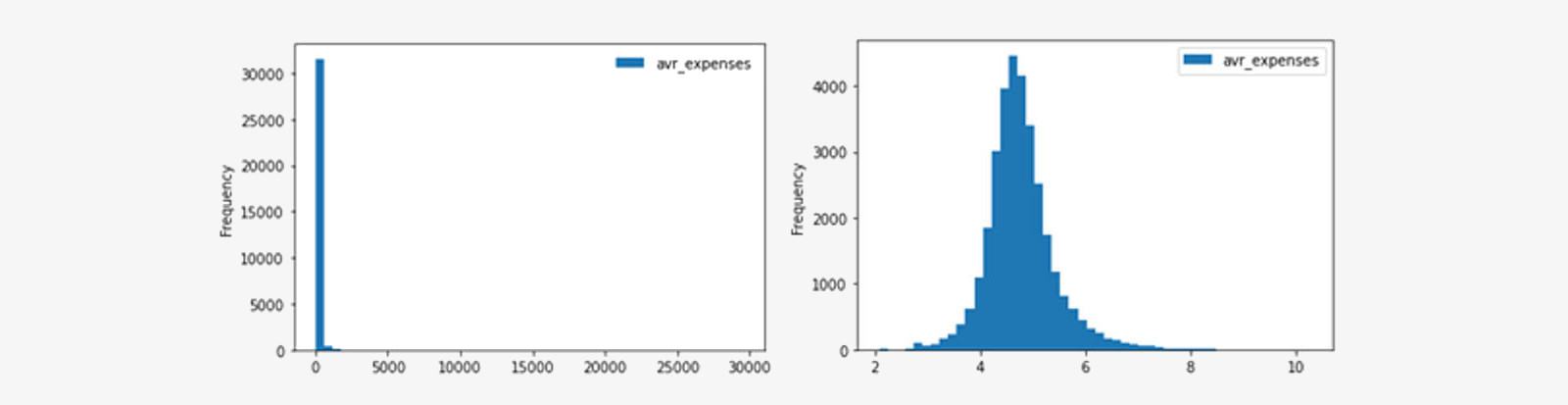
Ora è possibile iniziare il training della SOM con i dati ristrutturati e trasformati. La mappa originata contiene i codebook stimati, allocati in modo tale che codebook simili (vicini secondo la distanza euclidea) si trovino vicini sulla mappa 2-D.

Alcuni codebook:

La dimensionalità del vettore codebook è pari alla dimensionalità del dataset di input. Weight_2 – weight_11 sono i pesi relativi alle variabili dummy generate a partire da range età.

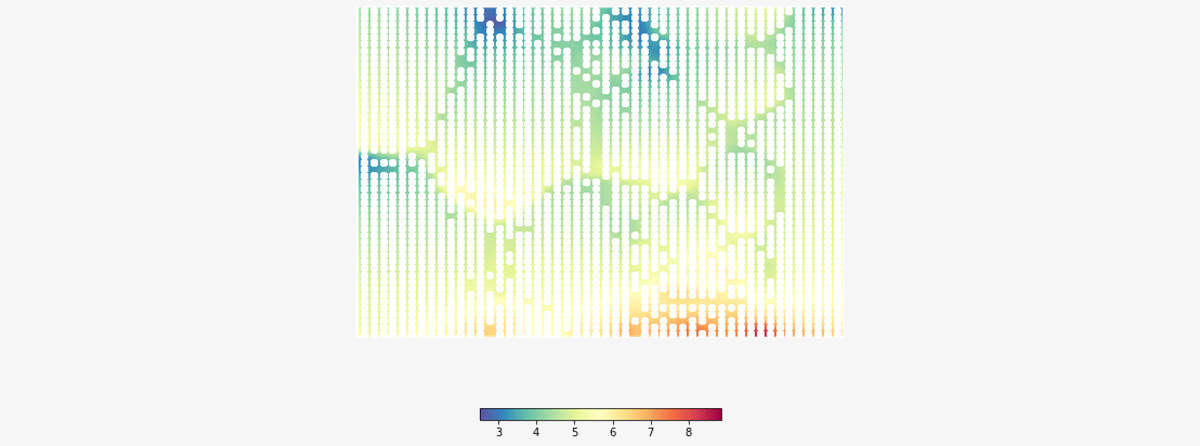
Sulla mappa è possibile visualizzare la distribuzione dei codebook relativi a ciascuna variabile. Ispezionando le distribuzioni è possibile individuare pattern (aree colorate) che descrivono il comportamento dei consumatori.

Nella seguente figura è riportata la SOM colorata rispetto ai pesi dei codebook relativi alla variabile spesa media (weight_0). I punti bianchi sono i codebook stimati:

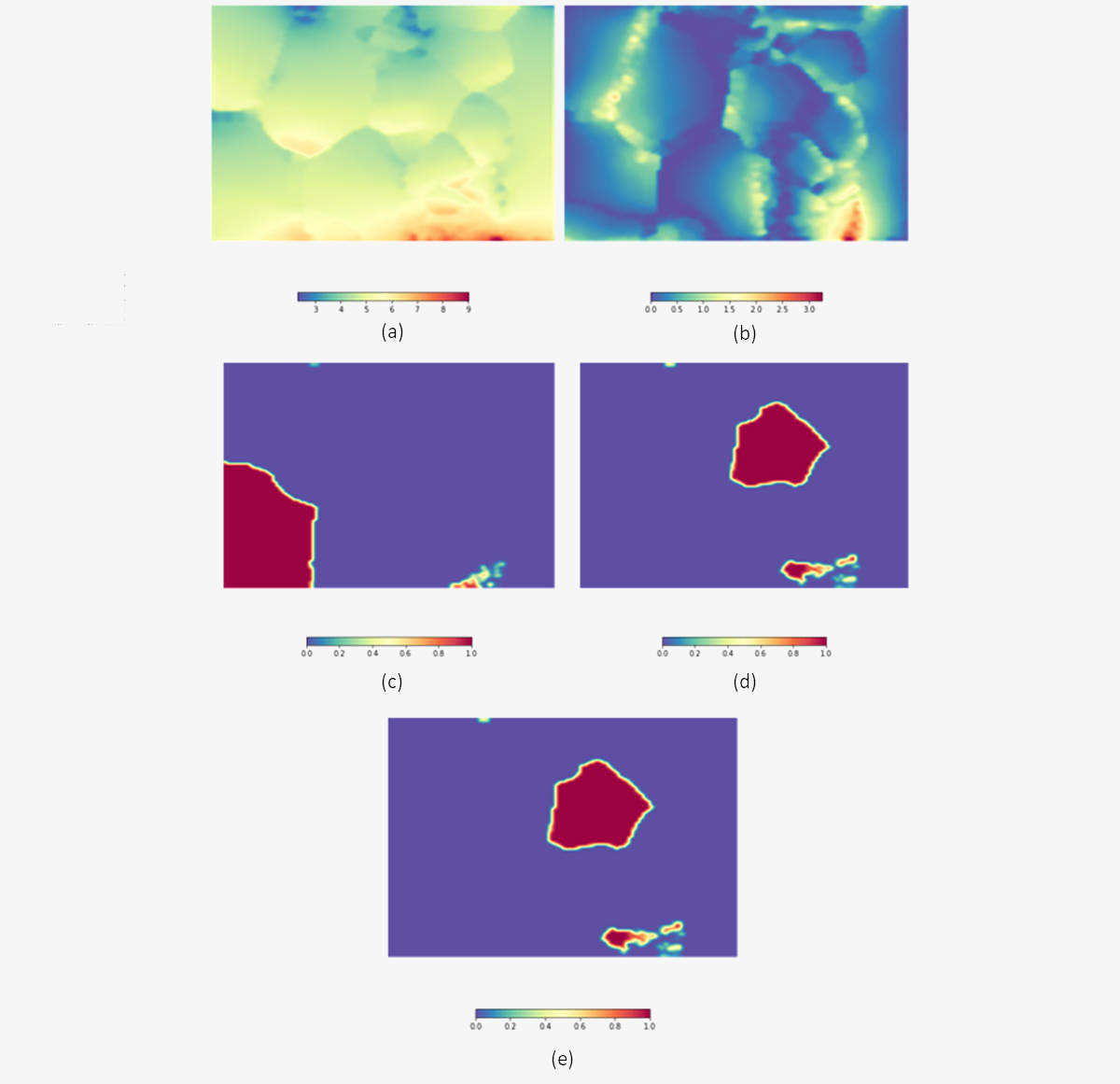
Nella figura sottostante, invece, la SOM è stata colorata secondo i pesi dei codebook relativi rispettivamente alle variabili (a) spesa media, (b) numero medio di prodotti acquistati, (c) range età 25-29, (d) range età 30-34, (e) range età 50-54. Si evince che in basso a destra si distribuiscono dei consumatori che spendono e acquistano molto ed hanno età compresa tra 50-54 anni e tra i 30 – 34 anni. Consumatori tra i 20-25 anni non spendono e non acquistano molto e sono collocati vicino ai consumatori tra i 30-34 anni. Infatti, la maggior parte dei consumatori nel range 30-34 ha spesa media e numero medio di acquisti non elevati, solo un piccolo gruppo rientra tra i consumatori “più attivi” citati sopra.

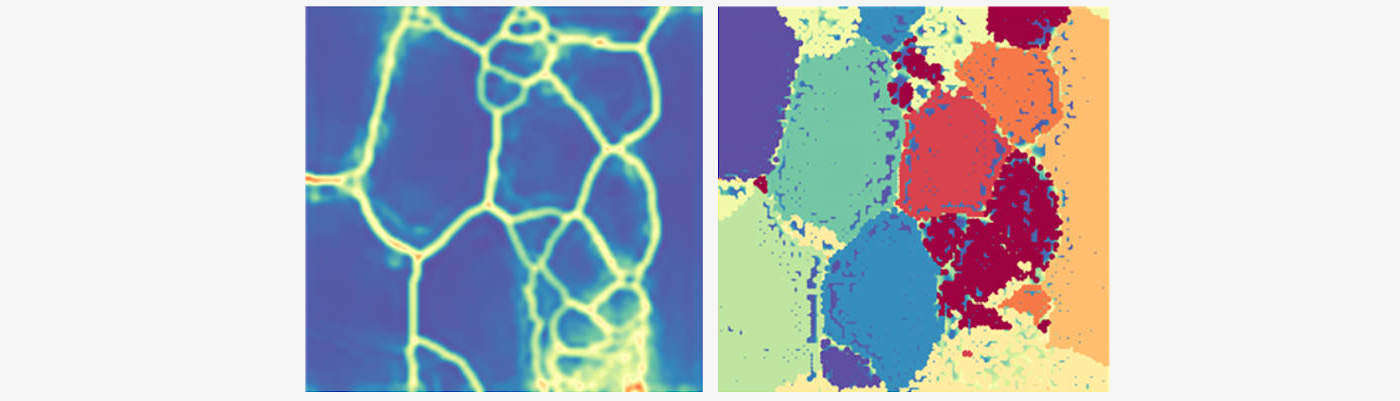
In seguito al training della SOM, è possibile visualizzare la U-Matrix dei codebook: la distanza euclidea tra i codebook è rappresentata in una scala di grigi o bicromatica in un’immagine 2-D . Il salto cromatico (rappresentato dal giallo nella figura sottostante a sinistra) indica codebook distanti, mentre l’altro colore più uniforme (in questo caso il blu) indica codebook vicini.

Infine, applicando un algoritmo di clustering sui codebook è possibile ottenere e visualizzare cluster di consumatori, come nella figura sottostante a destra.